은 십진법으로 표기했을 때 자리 수이고, 가장 높은 자리의 숫자는 이다.
양의 정수 , , 가 주어질 때, 부터 까지의 정수 중 4로 시작하는 2의 거듭제곱수의 개수를 구해 보자.
입력
첫째 줄에 양의 정수 , , 가 주어진다. ( )
인 경우만 주어진다.
출력
부터 까지의 정수 중 4로 시작하는 2의 거듭제곱수의 개수를 출력한다.
풀이
2의 거듭제곱의 첫 자리 숫자는 언뜻 보면 아무런 규칙도 없을 것 같다.
처음 이 문제를 보고 바로 든 생각은 로그인데, 수의 범위를 보아하니 그런 접근보다는 다른 접근이 필요해보인다.
일단 울며 겨자먹기로 2의 거듭제곱들의 맨 앞자리 숫자를 출력해보자....엇?

규칙이 있다! 주기라고는 할 수 없는데, 어떤 특정한 패턴이 반복되고 있다.
이 패턴들은 무조건 다음 5가지 중에 한 개이다.
(1, 2, 4, 8)
(1, 2, 4, 9)
(1, 2, 5)
(1, 3, 6)
(1, 3, 7)
이는 수학적으로 증명할 수 있다.
1. 어떤 수가 두 배가 될 때, 맨 앞자리 수 바로 다음 수가 5를 넘어가면 받아올림이 일어나며 맨 앞자리 수가 1 증가한다.
2. 그리고, 어떤 수가 두 배가 될 때 맨 앞자리 수가 5, 6, 7, 8, 9중 하나라면 무조건 두 배 했을 때의 맨 앞자리 수는 1이다.
이 두 가지 사실을 가지고, 받아올림이 일어날 수 있는 경우의 수를 세보자.

1부터 시작한다고 했을 때, 다시 1로 수가 돌아오기까지 나올 수 있는 패턴은 이렇게 5개임이 보여졌다.
그 다음으로, 우리는 한가지 관찰을 할 수 있다.
바로, 하나의 패턴이 끝나고 다시 맨 앞자리 수가 1로 돌아오게 되면 수의 전체적인 자릿수가 1 증가한다는 것이다!
그리고, 기가 막히게도 위의 5가지 패턴들 중 4가 포함되어있는 놈은 (1, 2, 4, 8), 그리고 (1, 2, 4, 9) 두 개밖에 없으며
이 두 패턴과 다른 패턴들과의 차이점은 바로 길이가 4라는 점이다.
그럼 결국에는 우리가 구해주어야하는 값은
(1, 2, 4, 8), (1, 2, 4, 9)의 패턴이 몇 번 등장했는가? 를 구해주면 되는 것이고
이는 주어진 수의 패턴이 끝나는 $n+1$(인덱스가 0부터 시작하기 때문에)에서 $3k$를 빼주면 된다!
그런데 문제는, 주어진 수의 패턴이 끝나는 지점이 언제인가...라는 것이다.
그러면 생각을 조금 바꾸어서, 주어진 수의 패턴 바로 전의 패턴의 $n+1$에서 $3(k-1)$를 빼주도록 하자.

이는 쉽게 구할 수 있는데,
수가 1로 시작하면 모든 5개의 패턴이 전부 1로 시작하므로 1을 빼주면 될 것이고
수가 2, 3으로 시작하면 모든 5개의 패턴의 두번째 수는 전부 2, 3이므로 2를 빼주면 될 것이고
수가 5, 6, 7로 시작하면 3을 빼주면 된다.
수가 4로 시작하면 해당 4도 세주어야하기 때문에 2만 빼주면 될 것이고
수가 8, 9로 시작하면 그 앞전에 나온 4도 세주어야 하기때문에 3을 빼주면 될 것이다.
이게 가능한 이유는 패턴들이 아래 사진과 같이 기똥차고 기합차게 생겼기 때문이다.
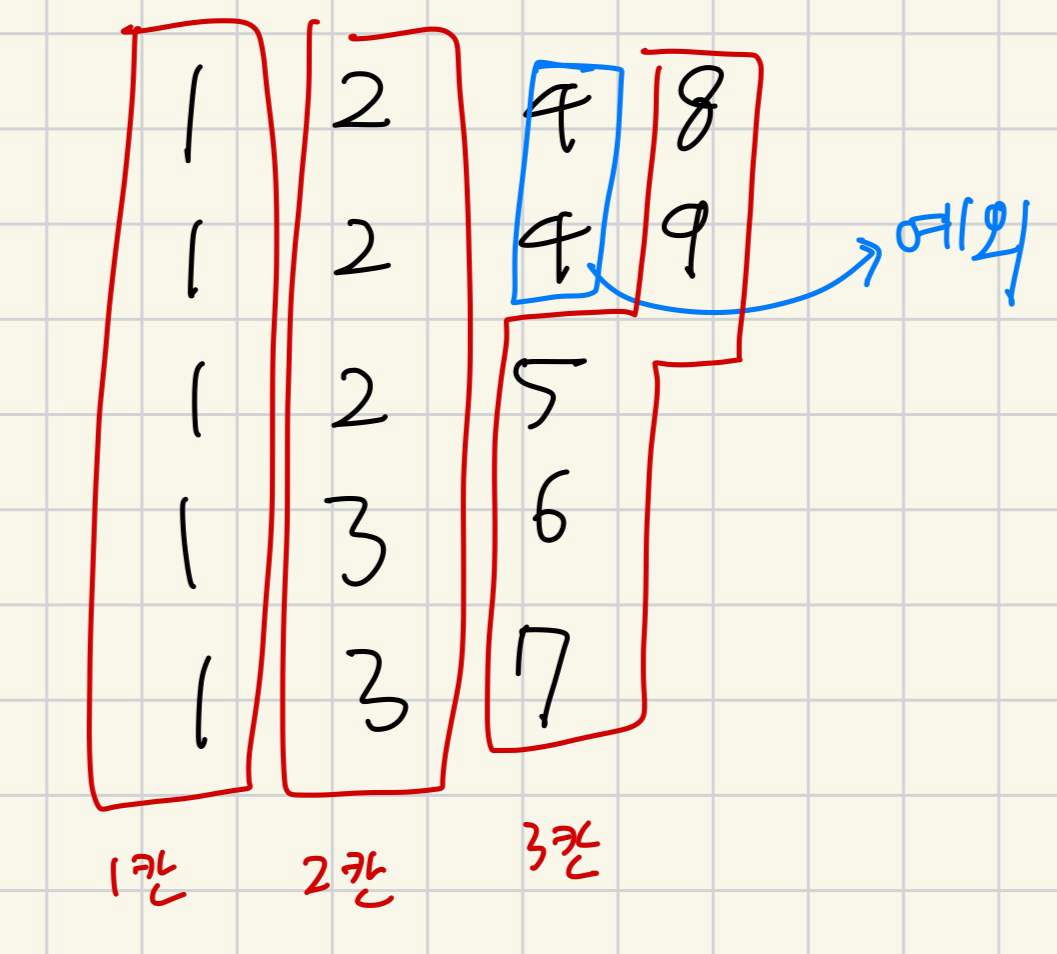
수가 무슨 숫자로 시작하는지는 X로 주어지기 때문에 이를 이용해서 계산할 수 있다.
그러면 코드를 이렇게 간단하게 짤 수 있다.
N, K, X = map(int, input().split())
if X in [1]:
print(N - 3*(K-1))
elif X in [2, 3, 4]:
print(N - 1 - 3 * (K - 1))
elif X in [5, 6, 7, 8, 9]:
print(N - 2 - 3 * (K - 1))
그리고 이건 추가적으로 든 생각인데,
1이 주어지면 0,
2, 3, 4가 주어지면 1,
5, 6, 7, 8, 9가 주어지면 2를 반환하는 함수를 찾아서 경우를 안나누고 한 번에 계산할 수도 있다.
내가 찾은 함수는 다음과 같다.
$$f(x) = \lceil \sqrt{x} \rceil - 1$$
그래서 경우를 안나누고 코드를 이렇게 짜는 것도 가능하다.
# 또는 이렇게도 할 수 있다
# 아예 1, 2, 3, 4, 5, 6, 7, 8, 9일때 각각 0, 1, 1, 1, 2, 2, 2, 2, 2를 반환하는 함수
from math import *
N, K, X = map(int, input().split())
print(N - 3*(K-1) - (ceil(sqrt(X)) - 1))
숏코딩 하신 다른 분들을 보면 정말 기똥찬 아이디어들이 많다.

'PS' 카테고리의 다른 글
| [Python] 백준 14517 - 팰린드롬 개수 구하기 (Large) (0) | 2025.04.25 |
|---|---|
| [Python] 백준 10220 - Self Representing Seq (0) | 2025.04.22 |
| [Python] 백준 3015 - 오아시스 재결합 (0) | 2025.04.21 |
| [Python] 백준 15824 - 너 봄에는 캡사이신이 맛있단다 (0) | 2025.04.21 |
| [Python] 백준 2243 - 사탕상자 (0) | 2025.04.21 |