[Python] 백준 13263 - 나무 자르기

kkigon 2025. 3. 24. 10:18

https://www.acmicpc.net/problem/13263

문제

높이가 a1, a2, ..., an인 나무 n개를 전기톱을 이용해서 자르려고 한다.

i번 나무에 전기톱을 사용할 때 마다 그 나무의 높이는 1만큼 감소한다. 전기톱은 사용할 때 마다 충전해야 한다. 전기톱을 충전하는 비용은 완전히 자른 나무의 번호에 영향을 받는다. 즉, 높이가 0이 되어버린 나무의 번호에 영향을 받는다. 완전히 잘려진 나무의 번호 중 최댓값이 i이면, 전기톱을 충전하는 비용은 bi이다. 완전히 잘려진 나무가 없다면 전기톱은 충전할 수가 없다. 가장 처음에 전기톱은 충전되어져 있다.

나무의 높이 ai와 각각의 나무에 대한 충전 비용 bi가 주어졌을 때, 모든 나무를 완전히 자르는데 (높이를 0으로 만드는데) 필요한 충전 비용의 최솟값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 둘째 줄에는 a1, a2, ..., an이, 셋째 줄에는 b1, b2, ..., bn이 주어진다. (1 ≤ ai ≤ 109, 0 ≤ bi ≤ 109)

a1 = 1이고, bn = 0이며, a1 < a2 < ... < an, b1 > b2 > ... > bn을 만족한다.

출력

나무를 완전히 자르는 충전 비용의 최솟값을 출력한다.

풀이

나만의 Convex Hull Trick 구현을 만들어보자.

나무 자르기 문제는 대표적인 Convex Hull Trick 기본 문제이다.

Convex Hull Trick, 줄여서 CHT는 일차함수꼴의 비용이 쭉 있고 이중에서 최소를 찾아서 dp에 저장해야하는, 딱 이 문제에 맞는 경우들에 쓸 수 있는 dp 최적화 기법이다.

지난번에 다른 블로그들의 도움을 받아서 이 문제를 푼 적이 있다. 하지만 그러면 절대로 실력이 늘지 않는 법. 직접 이 문제를 다시 연구하고 고민해서 나만의 CHT 를 만들지 않는 이상 실전에서 이걸 내가 스스로 짤 수 있을리가 없다.

먼저 문제부터 살펴보도록 하자.

문제에서는 모든 나무를 자르는 데 드는 비용이라고 나와있다.

그런데 B[N] = 0이므로, 결국에는 마지막 나무를 쓰러트리면 나머지 남은 나무들을 0의 비용으로 처리할 수 있을 것이므로 우리가 구하고자 하는 값은 마지막 나무를 쓰러트리는데 필요한 최소 비용일 것이다.

dp를 저장하는데, 맨 처음에 전기톱이 1 충전되어있으므로 dp의 값은 다음과 같이 저장하는 것이 좋을 것이다.

dp[i]는 i번째 나무를 1만큼만 남기고 잘랐을 때 드는 최소 비용. (다 자르고 나서 충전을 1만큼 다시 시켜놓는다)

당연히 dp[0](첫 번째 나무)는 0일 것이다. 아무것도 안해도 이미 1만큼 남아있으니까.

그 후, dp를 업데이트하는 수식은 다음과 같다.

i번째 나무를 자르기 바로 전에 j번째 나무를 자르고 왔다고 하자.

그러면 i번째 나무부터는 B[j]의 비용으로 자를 수 있을 것이다. 따라서 비용은

dp[i] = dp[j] + B[j] * (A[i] - 1) + B[j]

마지막에 B[j]를 한 번 더 더하는 이유는 다시 전기톱을 충전시켜놓은 상태로 대기시켜야 하니까.

그래서 정리하면

dp[i] = dp[j] + B[j] * A[i]

의 일차함수 꼴이 나오고, j는 0부터 i-1까지 돌면서 최소가 되는 값을 dp에 저장하면 될 것이다.

그러면 이 문제를 O(n^2) 안에 다음과 같이 풀 수 있다.

N = int(input())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

dp = [0] * N


# dp[i]는 i번째 나무를 1만큼만 남기고 잘랐을 때 드는 최소 비용
# dp[i] = min (a[i]b[j] + dp[j]), j는 0부터 i까지

# 가장 왼쪽 나무는 항상 높이가 0이므로 dp[0] = 0
# 가장 오른쪽 나무의 비용은 0이므로 구하고자 하는 값은 dp[-1]

# 그래서 원래는 N**2 복잡도로 이렇게 짤 수 있음

for i in range(1, N):
    tmp = 4318979203874
    for j in range(i):
        tmp = min(tmp, dp[j] + A[i]*B[j])
    dp[i] = tmp
print(dp[-1])

그런데 O(n^2) 풀이는 이 문제로 하면 시간초과가 나온다.

그래서, 오늘은 이 문제를 O(n log n)으로 최적화시키는 CHT에 대해서 소개한다.

예를 들어, 이렇게 여러 개의 일차함수가 있다고 하자.

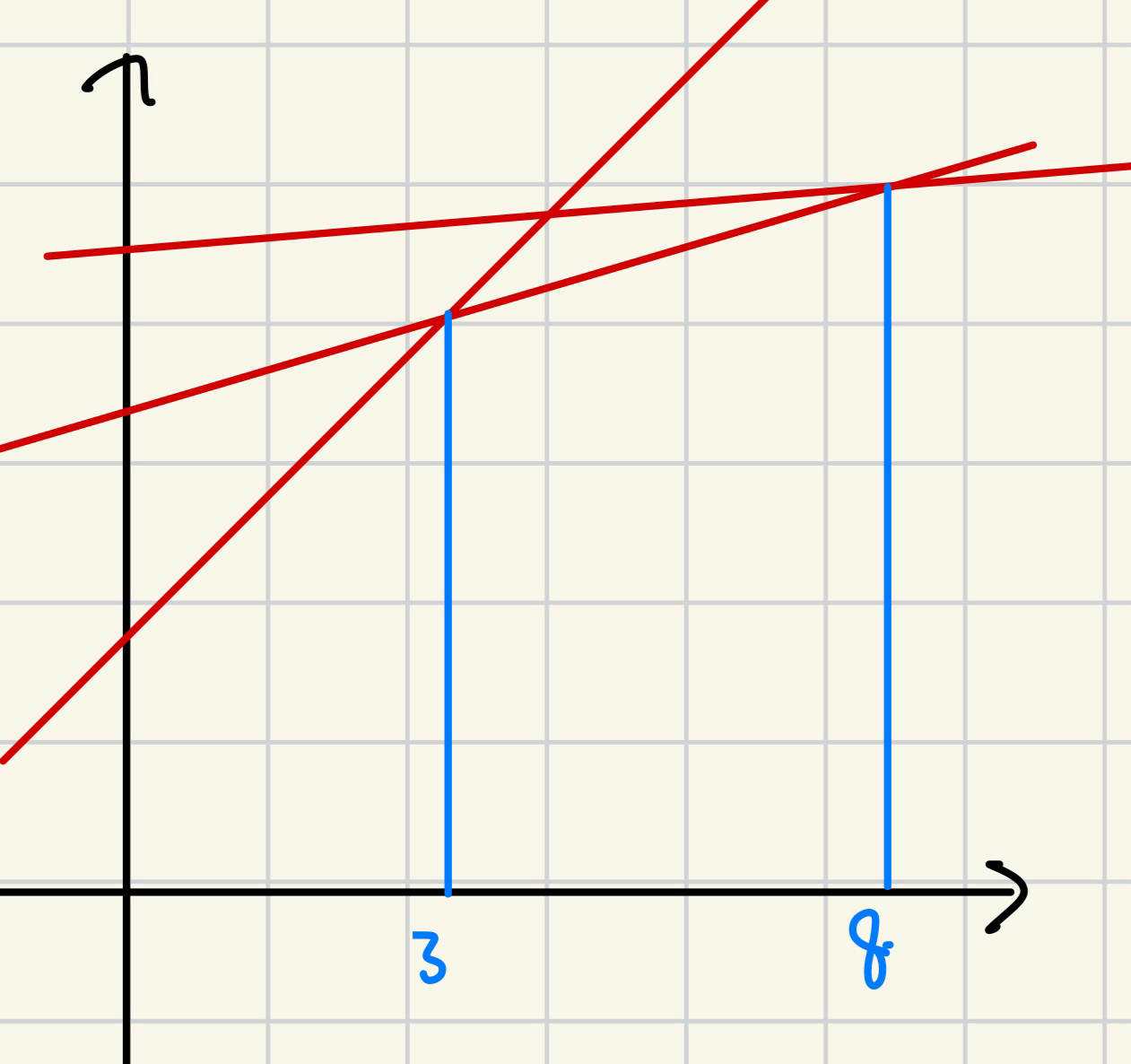
우리는 어떤 x좌표가 주어졌을 때 이 x좌표에서 값을 최소로 가지는 일차함수를 찾는 것이 목표라고 하자.

예를 들어 x=5에서 최소가 되는 함수를 찾는다고 하자.

x = 5에서는 일차함수가 3개가 정의되고, 그림처럼 생긴 3개의 점 중에서 최소의 점을 갖는 일차함수를 선택하면 될 것이다.

~~(이렇게 구하는 것이 아까 맨 처음에 작성한 O(n^2) 풀이이다)~~

하지만 우리는 다음과 같이 각 구간에서 최소가 되는, 마치 Convex Hull(볼록 껍질)과 같은 모양을 잡을 수 있다.

이 볼록 껍질에 대해서만 조사하면 우리는 최소가 되는 함수를 바로바로 찾을 수 있다.

그래서 이 볼록 껍질을 관리하기 위해서, 우리는 stack을 하나 만들고

이 stack에다가 함수를 다음과 같은 꼴로 저장해놓을 수 있다.

[기울기, y절편, 해당 구간의 시작점의 x좌표]

그러면 우리는 어떠한 x가 주어졌을 때, 이분 탐색을 통해 원하는 함수를 바로바로 찾을 수 있다!

총 N개의 쿼리에 대해서 log N 만에 원하는 값을 찾을 수 있어서, CHT 풀이는 O(N log N)이 되는 것이다.

이제 다시 문제로 돌아와보자.

아까 dp를 구할때

dp[i] = dp[j] + B[j] * A[i]

의 일차함수 꼴들 중에서 dp[i]가 최소가 되는 함수를 찾는 것이 목표였다.

A[i]가 주어졌을 때 여러개의 함수들 중 최소가 되는 것을 찾아야하니까 A[i]를 x값이라고 생각하면

y = dp[j] + B[j] *x

라는 일차함수들을 우리는 생각해줄 수 있다.

그래서 CHT로 풀 수 있다.

위의 아이디어를 그대로 코드로 구현해보자.

일단 dp는 처음에는 모두 0으로 초기화시켜준다.

dp = [0] * N

그리고 우리는 일차함수 두 개의 교차점의 x좌표를 찾는 함수가 하나 필요할 것이다.

# 일차함수의 교차점 x좌표 찾는 함수
def cross(f, g):
    return (g[1] - f[1])/(f[0] - g[0])

위 수식은 어렵지 않게 유도해낼 수 있다.

그리고 볼록껍질, 즉 여러 개의 일차함수들을 위에서 정의한대로 관리해주는 스택이 하나 필요하다.

이 문제의 경우 다른 나무들을 자르기 위해서 맨 처음 나무는 무조건 자르고 들어가야하니까, 스택에서 맨 처음 들어가있는 함수는 우리가 잡아줄 수 있다.

stack = [[B[0], dp[0], 0]]  # f들 관리하는 스택

예를 들어, 지금 스택에 들어가있는 함수는 기울기가 B[0]이고, y절편이 0인 y = B[0]x 이다.

이제 인덱스 1인 나무부터 마지막까지 나무를 돌면서 다음을 반복해주면 될 것이다.

1. 나무 자르기

2. 새로운 함수 추가하기

1. 나무 자르기 단계는 함수들을 돌면서 최소가 되는 함수를 이분 탐색으로 찾아 dp에 넣어주는 과정이 될 것이고,

2. 새로운 함수 추가하기 단계는 이제 새로운 나무 하나를 다 잘랐으니 앞으로 이 나무의 비용을 쓸 수 있도록 새로운 일차함수를 스택에 추가해주는 과정이라고 보면 되겠다.

for i in range(1, N): #두 번째 나무부터 시작
    X = A[i]

    stack_index = bisect_left(stack, X, key = lambda x: x[2]) - 1
    dp[i] = X * stack[stack_index][0] + stack[stack_index][1]

이분 탐색은 귀찮으니까 직접 구현하지 않고 python 기본 내장 모듈인 bisect를 사용해줄 수 있다.

오늘 처음 알았는데, bisect_left에서 key를 따로 정해줄 수 있더라. 그래서 우리는 쉽게 일차함수들을 찾아줄 수 있다.

bisect_left를 한 다음 인덱스에서 1을 빼줘야 우리가 쓸 수 있는 최소의 비용 함수를 찾을 수 있을 것이다.

그리고, 우리는 구한 값을 dp에 저장해줄 수 있다.

이제 새로운 함수를 추가해보자.

for i in range(1, N): #두 번째 나무부터 시작
    X = A[i]

    stack_index = bisect_left(stack, X, key = lambda x: x[2]) - 1
    dp[i] = X * stack[stack_index][0] + stack[stack_index][1]

    # 이제 나무를 다 잘랐으니 새로운 함수를 추가해보자.
    f = [B[i], dp[i], 0]
    tmp = cross(f, stack[-1])
    f[2] = tmp
    stack.append(f)

stack의 가장 마지막에 들어있는 원소와의 교차점을 구한 다음, 이 정보를 이용해서 새로운 함수 f를 만들고 스택에 넣어주면 될 것이다.

그런데 여기서 문제가 하나 있다.

예를 들어 다음과 같은 함수가 새로 추가되었다고 하자.

이런 경우에는 원래 있었던 2번째 함수가 아무런 의미가 없어지게 된다. 우리는 스택에서 이 쓸모없는 함수를 빼주고 교차점 데이터를 갱신해줄 필요가 있다!

그래서, 일단 함수를 추가해준 다음에

만약 현재 스택에 함수가 3개 이상 있고, 원래 있던 두 개의 함수의 교차점이 현재 함수와 원래 있던 가장 최근의 함수의 교차점보다 큰 동안에는

스택에서 마지막에서 두번째 원소(원래 있었던 쓸모없는 함수)를 while 문을 통해 빼줄 수 있다.

다 빼주고 난 다음에는 교차점의 좌표를 갱신해야할 것이다.

이는 다음과 같이 구현할 수 있다.

# 그런데 쓸모없는 함수가 생길지도 모르니까
while len(stack) >= 3 and cross(stack[-3], stack[-2]) > cross(stack[-2], stack[-1]):
    stack.pop(-2)
stack[-1][2] = cross(stack[-1], stack[-2])

자. 모든 과정이 끝났다. CHT, 생각보다 간단하지 않은가? 이제 전체 코드를 보자!

N = int(input())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

dp = [0] * N


# dp[i]는 i번째 나무를 1만큼만 남기고 잘랐을 때 드는 최소 비용
# dp[i] = min (a[i]b[j] + dp[j]), j는 0부터 i까지

# 가장 왼쪽 나무는 항상 높이가 0이므로 dp[0] = 0
# 가장 오른쪽 나무의 비용은 0이므로 구하고자 하는 값은 dp[-1]

# 그래서 원래는 N**2 복잡도로 이렇게 짤 수 있음

# for i in range(1, N):
#     tmp = 4318979203874
#     for j in range(i):
#         tmp = min(tmp, dp[j] + A[i]*B[j])
#     dp[i] = tmp
# print(dp[-1])

# 하지만, 이걸 컨벡스 헐 트릭으로 O(nlogn)까지 줄여보자는 마인드.

# 일차함수의 교차점 x좌표 찾는 함수
def cross(f, g):
    return (g[1] - f[1])/(f[0] - g[0])

# j들에 대해서 탐색해야하므로 f(x) = b[j]x + dp[j]
# 함수는 [기울기, y절편, 시작점의 x좌표]
from bisect import *
stack = [[B[0], dp[0], 0]]  # f들 관리하는 스택
for i in range(1, N): #두 번째 나무부터 시작
    X = A[i]

    stack_index = bisect_left(stack, X, key = lambda x: x[2]) - 1
    dp[i] = X * stack[stack_index][0] + stack[stack_index][1]

    # 이제 나무를 다 잘랐으니 새로운 함수를 추가해보자.
    f = [B[i], dp[i], 0]
    tmp = cross(f, stack[-1])
    f[2] = tmp
    stack.append(f)

    # 그런데 쓸모없는 함수가 생길지도 모르니까
    while len(stack) >= 3 and cross(stack[-3], stack[-2]) > cross(stack[-2], stack[-1]):
        stack.pop(-2)
    stack[-1][2] = cross(stack[-1], stack[-2])

print(dp)
print(stack)
print(dp[-1])

주석을 모두 제거하면 다음과 같이 깔끔한 코드로도 나타낼 수 있다.

from bisect import *

N = int(input())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

dp = [0] * N

def cross(f, g):
    return (g[1] - f[1])/(f[0] - g[0])

stack = [[B[0], dp[0], 0]]
for i in range(1, N):
    X = A[i]
    idx = bisect_left(stack, X, key = lambda x: x[2]) - 1
    dp[i] = X * stack[idx][0] + stack[idx][1]
    f = [B[i], dp[i], 0]
    tmp = cross(f, stack[-1])
    f[2] = tmp
    stack.append(f)

    while len(stack) >= 3 and cross(stack[-3], stack[-2]) > cross(stack[-2], stack[-1]):
        stack.pop(-2)
    stack[-1][2] = cross(stack[-1], stack[-2])

print(dp[-1])

고급진 기술인데 생각보다 별 내용이 없어서 놀랐다!

'PS' 카테고리의 다른 글

[Python] 백준 4008 - 특공대 (0)	2025.03.24
[Python] 백준 14751 - Leftmost Segment (0)	2025.03.24
[Python] 백준 9892 - Width (0)	2025.03.23
[Python] 백준 10254 - 고속도로 (0)	2025.03.23
[Python] 백준 1708 - 볼록 껍질 (0)	2025.03.23

현재글[Python] 백준 13263 - 나무 자르기

아롱이의 PS하는 블로그

PS 다시 시작!

아롱이의 PS하는 블로그