두 자연수 A, B가 주어졌을 때, A ≤ x ≤ B를 만족하는 모든 x에 대해 x를 이진수로 표현했을 때 1의 개수의 합을 구하는 프로그램을 작성하시오.
즉, f(x) = x를 이진수로 표현 했을 때 1의 개수라고 정의하고, 아래 식의 결과를 구하자.
$$\sum_{x=A}^{B}{f(x)}$$
입력
첫 줄에 두 자연수 A, B가 주어진다. (1 ≤ A ≤ B ≤ ((10^{16})))
출력
1의 개수를 세어 출력한다.
풀이
사실 누적합, dp 그런거 다 필요없다.
약간의 관찰을 하면 자리수별로 1의 개수를 직접 계산할 수 있다!
일단 A, B를 받는다.
그리고, 0부터 N까지 1의 개수를 카운팅하는 함수 sol()를 만들고, 최종적인 결과로 sol(B) - sol(A-1)을 출력하도록 하자.
좋다. 이제 어떤 수 N을 받았을 때 (( \sum_{x=0}^{N}{f(x)} ))을 계산하는 sol()을 만들어보자.
관찰해보자.
예시로 주어진 12를 보자.
12는 이진수로 1100이다.
0부터 12까지 이진수를 쫙 써보자.

그런데 잘 보면 규칙이 있다.
한 번 묶어보자.
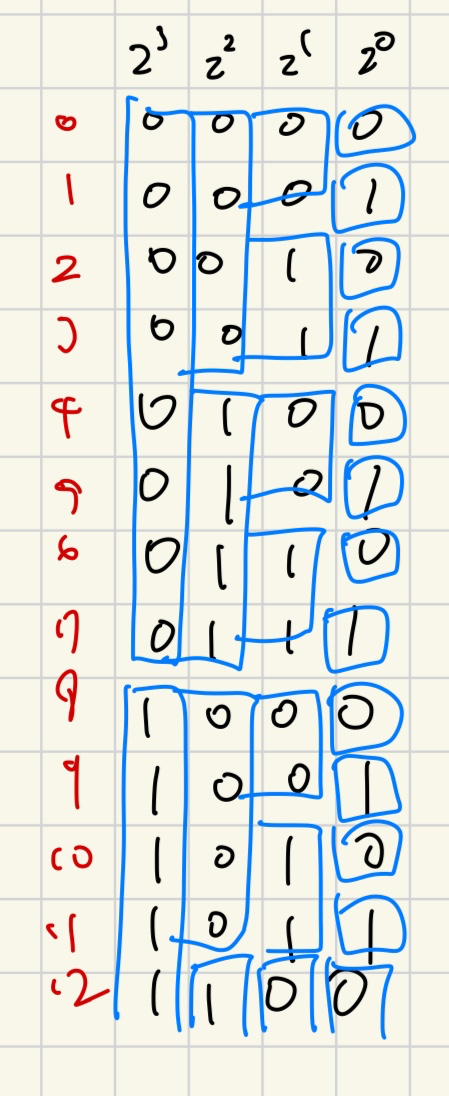
아하. 2^n에 해당하는 자리수는 2^n개씩 0과 1이 묶여서 나오는구나.
이걸 응용해서 1의 개수를 세주는 것은 코드로 쉽게 할 수 있을 것이다.
계산식은 설명하기 귀찮아서 생략한다.
아래에는 코드만 첨부한다.
A, B = map(int, input().split())
def sol(N):
N += 1
cnt = 0
size = 1
while size < N:
size <<= 1
while size >= 2:
cnt += (N // size) * (size//2)
if N // (size // 2) % 2 == 1:
cnt += N % (size // 2)
size //= 2
return cnt
print(sol(B) - sol(A-1))
'PS' 카테고리의 다른 글
| [Python] 백준 15824 - 너 봄에는 캡사이신이 맛있단다 (0) | 2025.04.21 |
|---|---|
| [Python] 백준 2243 - 사탕상자 (0) | 2025.04.21 |
| [Python] 백준 1419 - 등차수열의 합 (0) | 2025.04.04 |
| [Python] 백준 3679 - 단순 다각형 (0) | 2025.03.31 |
| [Python] 백준 30645 - 인형 전시 (0) | 2025.03.29 |