"파이썬으로 구현하는"
시리즈 3
매내처
(Manacher)
오늘은 갑자기 뜬금없이 파이썬으로 구현하는 매내처에 대해서 알아볼 것이다.
원래는 세그먼트 트리 바텀업을 먼저 적었어야 했는데, 문제풀다가 매내처라는 천재적인 알고리즘을 공부하게 되어서 정리해본다.
먼저 매내처가 뭐하는 알고리즘인지 알아보자.
팰린드롬이란 무엇인가?
앞뒤가 대칭인 문자열을 팰린드롬이라고 한다. 우리말로 회문이라고 한다.
예시로는 다음이 있다.
'bob'
'ABCBA'
'WAS IT A CAT I SAW' (이상한 나라의 앨리스에 나오는 유명한 회문)
'다시합창합시다'
다음과 같은 예시들은 팰린드롬이 아니다.
'apple'
'팰린드롬'
'알고리즘'
매내처는 팰린드롬을 다루는 알고리즘인데, 구체적으로는 다음과 같은 문제를 풀 때 쓰인다.
문자열 S가 주어질 때, S의 부분 문자열 중 최장 길이의 팰린드롬을 구해보자.
(사실 매내처는 이 문제에서만 쓰이는, 오직 이 문제를 풀기 위해서 만들어진 알고리즘이다)
보통 이 문제를 O($n^2$) 안에 dp를 이용해서 쉽게 풀 수 있다.
그러나, 매내처는 이 문제를 O($n$) 안에 풀 수 있다.
매내처의 아이디어는 다음과 같다.
먼저, 팰린드롬을 저장하는 새로운 방식에 대해서 생각해보아야 한다.
매내처에서는, 중심 인덱스와 그 인덱스가 가지는 팰린드롬 반지름 중 가장 큰 것을 P 배열에 저장한다.
예시를 통해 알아보자.

가장 가운데에 있는 c의 인덱스가 i일 때, P[i] = 3이다. 이해가 쏙쏙 되지 않는가?
그런데 이렇게 하면 문제가 생긴다. abccba처럼 짝수 길이의 팰린드롬은 어떻게 저장하는가?
이 문제를 방지하기 위해 우리는 문자열에 전처리를 할 것인데, 바로 빈 공간 사이사이에 #과 같은 쓸데없는 더미 문자를 추가해주는 것이다.
그러면 abccba는 #a#b#c#c#b#a#가 되었고, 모든 팰린드롬들이 홀수 길이가 되었으므로 우리는 이 문자열에 대해서 위의 방법을 사용해줄 수 있다.
어쨌든, 이 아이디어를 이해했다고 보고 매내처의 핵심 아이디어를 살펴보자.
매내처의 핵심 아이디어를 한 줄로 표현하면 다음과 같다.
“이미 찾아둔 ‘가장 오른쪽까지 뻗는 팰린드롬’을 거울삼아,
새 중심의 반지름을 공짜로 추정→확장만 하면 된다.”
우선, 두 개의 값 C, R을 정의할 것이다. C는 지금까지 찾은 팰린드롬 중 가장 오른쪽까지 뻗어있는 팰린드롬의 중심 인덱스이고, R은 그 팰린드롬의 오른쪽 끝 인덱스이다. 아래 그림을 통해 이해해보자. 편의상 #은 일단 생각하지 말아보자.
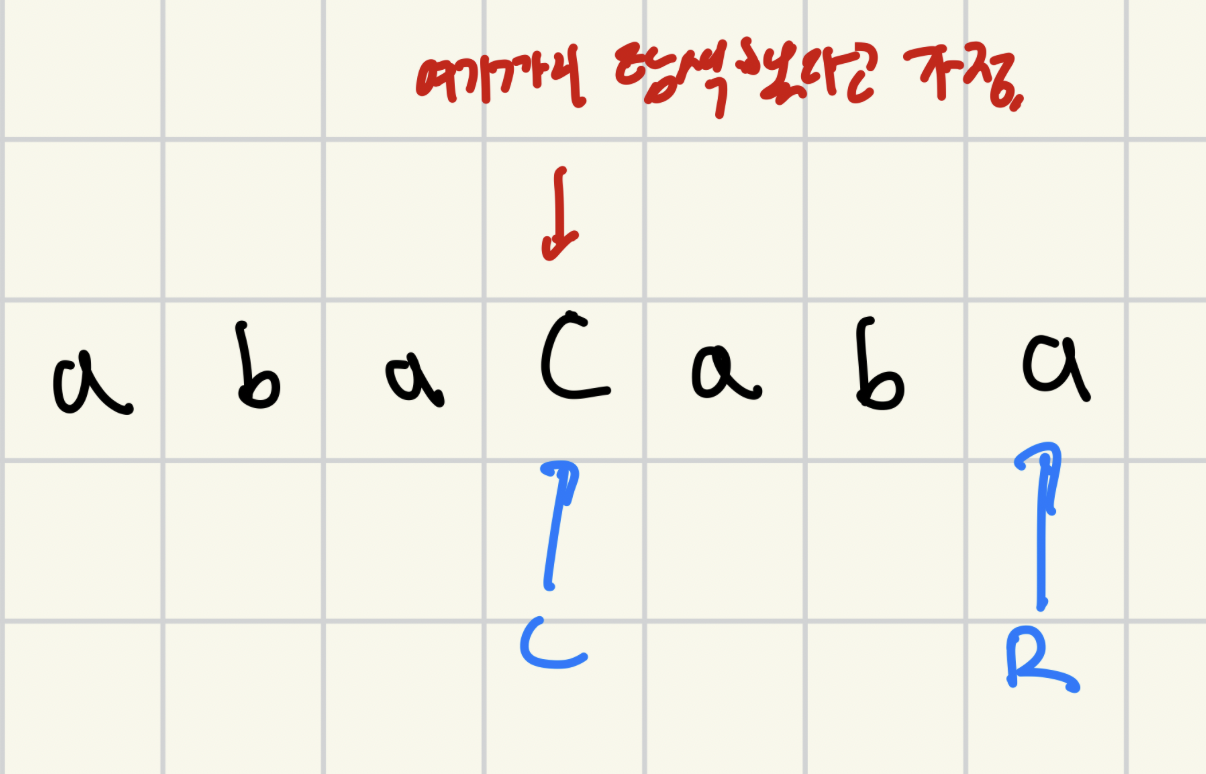
R, C의 초기값은 0, 0이다.
여기까지 파이썬으로 짜보면 다음과 같다.
S = input()
t = '#' + '#'.join(S) + '#'
N = len(t)
P = [0] * N
R = C = 0
이제, 전처리된 문자열에 대해서 인덱스 0부터 N(전처리된 문자열의 길이)에 대해서 for 루프를 돌아줄 것이다.
a b a c a b a를 예시로 들어보자. 가운데 c를 중심으로 양쪽으로 a b a, a b a가 같다. 이는 팰린드롬의 성질이다. 그러니까, 우리는 c 오른쪽에 있는 인덱스들에 대해서 P 배열을 채워줄 때 거울처럼 이미 찾아준 왼쪽의 인덱스들을 최대한 그대로 이용해보자는 것이다.
지금 탐색하고 있는 인덱스를 i라고 해보자.
만약 i < R이라면, (지금까지 찾은 가장 긴 팰린드롬 안에 탐색 범위가 포함, 위의 '거울 원리'를 쓸 수 있을 때)
P[i] = min(R - i, P[2*C - i])라고 일단 해줄 수 있다. 일단 해두었다는 것은 이것이 최대 길이가 아닐 수 있다는 것이다.

mirror = 2*C - i
if i < R:
P[i] = min(R - i, P[mirror])그 다음에 우리는 이 P[i] 값보다 팰린드롬이 더 길어질 수 있을지 while 문으로 돌아볼 것이다.
while i - P[i] - 1 >= 0 and i + P[i] + 1 < N and t[i - P[i] - 1] == t[i + P[i] + 1]:
P[i] += 1
그런 다음, 혹시나 C, R 값이 바뀌었을 수도 있으니까 업데이트를 해준다.
if i + P[i] > R:
C, R = i, i + P[i]
놀랍게도 이 간단하고 천재적인 아이디어로
짧은 코드를 작성하였고, 매내처의 구현은 끝났다.
S = input()
t = '#' + '#'.join(S) + '#'
N = len(t)
P = [0] * N
R = C = 0
for i in range(N):
mirror = 2*C - i
if i < R:
P[i] = min(R - i, P[mirror])
while i - P[i] - 1 >= 0 and i + P[i] + 1 < N and t[i - P[i] - 1] == t[i + P[i] + 1]:
P[i] += 1
if i + P[i] > R:
C, R = i, i + P[i]
앞으로 문제를 풀면서 P 배열을 어떻게 쓰는지는 당신의 손에 달려있다.
다만, 여기서 구한 P 배열은 #으로 전처리된 문자열에 대해 만들어진 것임을 잊지 말도록 하라.
대표적인 연습문제로는
가장 긴 팰린드롬 부분 문자열
https://www.acmicpc.net/problem/14444
https://www.acmicpc.net/problem/13275
(2개가 똑같은 문제이다. 14444는 솔브닥에서 레이팅을 안 준다.)
#15164번_제보
https://www.acmicpc.net/problem/16163
팰린드롬??
https://www.acmicpc.net/problem/11046
(매내처 + 쿼리)
등이 있다.
'파이썬으로 구현하는 시리즈' 카테고리의 다른 글
| [파이썬으로 구현하는] 분할 정복을 이용한 거듭제곱 (0) | 2025.05.17 |
|---|---|
| [파이썬으로 구현하는] 세그먼트 트리(Segment Tree) - Bottom-Up (0) | 2025.05.14 |
| [파이썬으로 구현하는] 세그먼트 트리(Segment Tree) - Top-Down (0) | 2025.04.11 |
| [파이썬으로 구현하는] 분리 집합(Disjoint Set) (0) | 2025.04.05 |