https://www.acmicpc.net/problem/18122
https://www.acmicpc.net/problem/27743
풀이
충분히 찍어서 맞출 수 있는 문제이다.
일단 일반적으로 하노이 탑 N개를 옮기는 최소 횟수는 $2^{N} - 1$회임이 잘 알려져있다.
그런데 18122번 문제와 같은 경우는 어떻게 하면 좋을까?
일단 N = 1일 때를 살펴보자.

그림과 같이 3회를 옮기면 됨을 알 수 있다.
N = 2일 때는 어떨까?

일단 위에 쌓여있는 쪼그만 놈들은 무시하고, 큰 1, 2번 판이 어떤 움직임을 보여야 하는지 생각해보자.
그러면 N = 1일때와 마찬가지의 방법으로 3번 움직여야 함을 알 수 있다.

이제 쪼그만 놈들의 움직임을 보자. 큰 판들이 위와 같이 잘 움직일 수 있게 쪼끄만 놈들을 어떻게 움직여야하나 살펴보면...
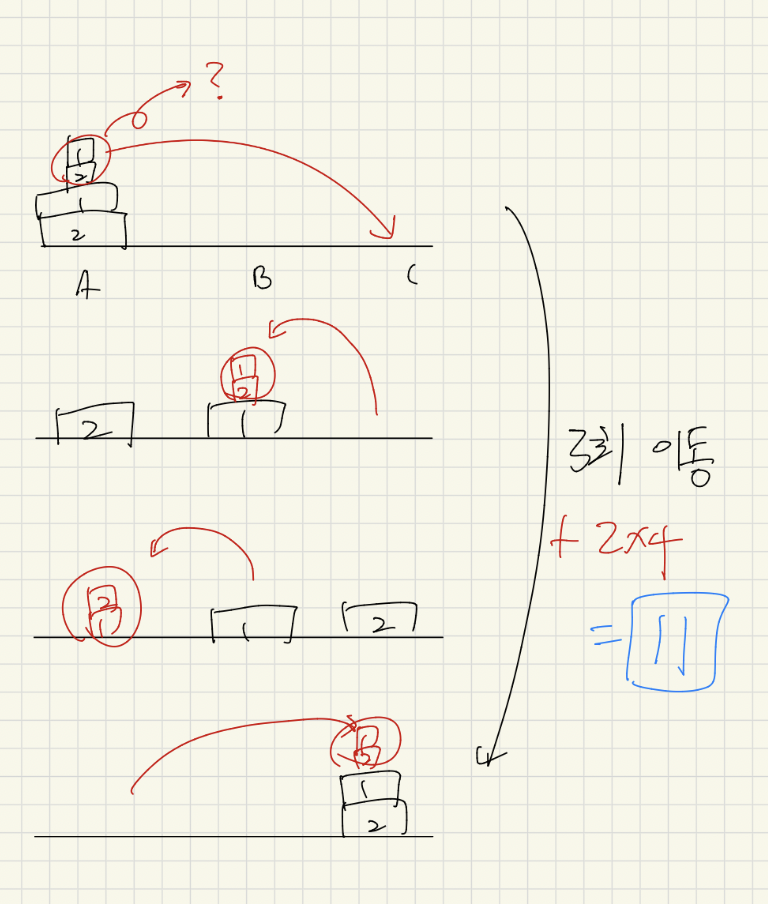
4번 움직여야 함을 알 수 있다.
쪼끄만놈 한뭉탱이를 옮기는 데에 2번의 움직임을 쓰니까
전체 움직인 횟수는 3 + 2*4 = 11번이다.

만약 N = 3일때는 어떻게 하면 좋을까?
위 상황에서 더 쪼끄만 뭉탱이가 더 쌓여있다고 생각하자.
그러면 여기서 일반적인 하노이탑을 옮기듯이 2*8번을 더 움직여야 함을 알 수 있다.
그러니까 최종 답은...
3 + 2*4 + 2*8 + 2*16 + 2*32......
식을 정리하면
$ 2\times (2^{N+1} - 2) - 1$
이다.
그래서 18122번의 정답은 다음과 같다.
N = int(input())
ans = 2*(2**(N+1) - 2) - 1
print(ans % 1_000_000_007)
조금 더 일반적으로, 27743번을 살펴보자.
2개씩이 아니라 M개가 쌓여있다면...
단순히 앞의 계수만 2가 아니라 M으로 바꿔주면 된다.
$ M\times (2^{N+1} - 2) - 1$
다만 이 식을 쓰면 M == 1 일 때(그냥 기본 하노이탑) 식이 성립을 안 해서 따로 처리해주면 된다.
N, M = map(int, input().split())
MOD = 1_000_000_007
ans = 0
if M == 1:
ans = pow(2, N, MOD) - 1
else:
ans = M * (pow(2, N+1, MOD) - 2) - 1
print(ans % MOD)


'PS' 카테고리의 다른 글
| [Python] 백준 8481 - Generator (0) | 2025.08.20 |
|---|---|
| [Python] 백준 1533 - 길의 개수 (0) | 2025.08.18 |
| [Python] 백준 1086 - 박성원 (1) | 2025.08.05 |
| [C++] 백준 1106 - 호텔 (0) | 2025.08.04 |
| [Python] 백준 16995 - Piece of Cake (2) | 2025.08.02 |