이 문제는 백준 14505 팰린드롬 개수 구하기 (Small)과 N의 범위만 다르고 똑같은 문제입니다.
(그런데 Small 알고리즘은 생각 안나고 이 풀이가 먼저 바로 생각나서 그냥 Small도 이렇게 품..ㅋㅋㅋ)
https://www.acmicpc.net/problem/14517
https://www.acmicpc.net/problem/14505
문제
팰린드롬(palindrome)이란 앞에서부터 읽으나 뒤에서부터 읽으나 같은 단어를 말한다. 'aba'나 'a'와 같은 단어는 팰린드롬이며, 'abaccbcb'나 'anavolimilana'와 같은 단어는 팰린드롬이 아니다.
승수는 주어진 문자열의 부분수열 중 팰린드롬이 되는 부분수열의 개수를 알고싶어한다. (공집합은 포함하지 않는다)
예를들어 'abb' 의 부분수열은 {'a'}, {'b'}, {'b'}, {'ab'}, {'ab'}, {'bb'}, {'abb'} 이고 이 가운데 팰린드롬은 {'a'}, {'b'}, {'b'}, {'bb'} 으로 4개 이다.
문자열이 주어졌을 때, 팰린드롬이 되는 부분수열의 개수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 길이가 1000(small은 30임)을 넘지 않는 문자열 S 가 주어진다. 문자열 S는 알파벳 소문자로만 이루어져 있다.
출력
주어진 문자열 S 의 부분수열 중 팰린드롬이 되는 부분수열의 개수를 10,007 로 나눈 나머지를 출력한다.
풀이
우리가 보통 dp로 문자열 안에서 팰린드롬인지를 비교할 때 어떻게 하는가?
이전에 올린 글 중 이 글을 참고하라.
아마 이 방법을 조금 변형하면 되지 않을까 싶은데...
예시를 들어보자. 예시는 abaccbcb로 들어보겠다.
일단 dp를 어떻게 만들어줄 것이냐면,
2차원 리스트로 만들 것인데 다음과 같이 길이(반복문으로 할 수 있게끔), 시작 인덱스를 기준으로 만들어 줄 것이다. 참고로 길이 0은 편의상 1글자로 생각한다.
#dp[l][i] = True이면 S[i:i+l+1]은 팰린드롬임
dp = [[None]*N for _ in range(N)]
l이 작은 값부터 시작해서 채워나가면 이 값들을 재활용할 수 있다.
예를 들어 아래 그림에서 빨간 화살표가 가리키는 구간에서 팰린드롬의 개수를 세고 싶다고 하자.

그러면 여기서 길이가 1 작은 것을 2개 생각할 수 있을 것이다.(아래 그림에서 파란색 1, 2)
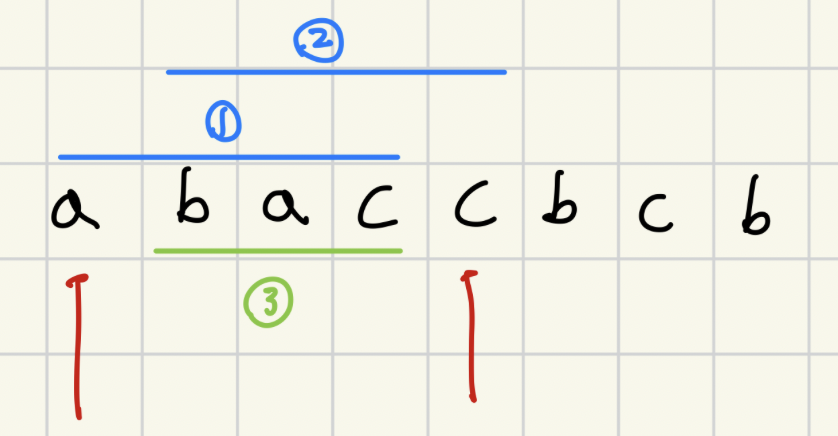
파란색 1, 2를 더해주면 3번 부분이 중복처리된다. 그래서 한 번 빼줘야 한다.
이것이 바로 이 문제에 포함배제의 원리 태그가 붙은 이유이다.
그런데, 만약 1의 시작점과 2의 끝부분이 같은 문자이면 어떡하는가? 가령 다음과 같은 경우처럼.
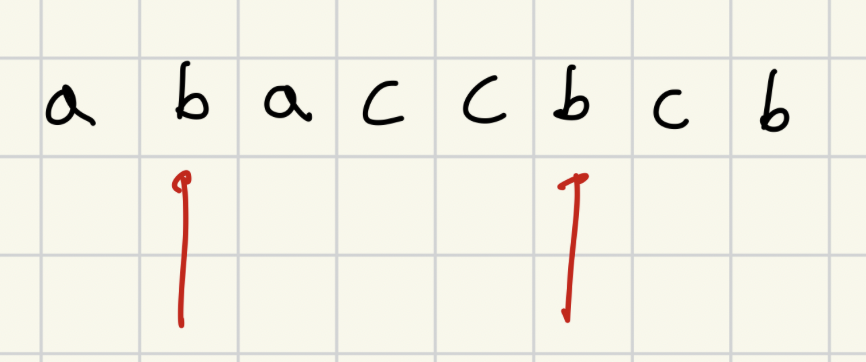
그러면 우리는 아래 그림과 같이 두 가지를 추가로 생각해줄 수 있는데,
b, b 두개만으로도 새로운 팰린드롬을 만들 수 있다는 점과
b, b 사이에 낀(a, c, c) 것들 양 끝에 b, b를 붙여서 새로운 팰린드롬을 또 만들 수 있으니
이 값들을 추가로 더해주어야 한다.

dp의 초기값은 어떻게 구성하는가?
길이가 0(1글자면) 팰린드롬이 그 자체로 1개밖에 없으니 1로 설정한다.
길이가 1(2글자면) 경우를 나누어 다음과 같이 설정한다.
1. 두 글자가 다른 경우 -> 2
2. 두 글자가 같은 경우 -> 3
그리고 이중 반복문을 돌며 $l$의 길이를 늘려가며 dp를 채우고,
정답으로는 dp[-1][0]을 10007로 나눈 나머지를 출력하면 쉽게 풀린다.
(그리고 이 코드에서 10007로 나눈 나머지 처리를 안해주면 14505번 문제의 정답이 된다.)
14505번 문제의 출제자 의도 풀이를 아는 사람이 있으면 누가 댓글로 좀 알려주세요
S = input()
N = len(S)
#dp[l][i] = True이면 S[i:i+l+1]은 팰린드롬임
dp = [[None]*N for _ in range(N)]
cnt = 0
for l in range(N):
for i in range(N - l):
if l == 0:
dp[l][i] = 1
elif l == 1:
dp[l][i] = 2
if S[i] == S[i+l]:
dp[l][i] += 1
else:
dp[l][i] = dp[l - 1][i] + dp[l - 1][i + 1] - dp[l - 2][i + 1]
if S[i] == S[i+l]:
dp[l][i] += 1 + dp[l-2][i+1]
print(dp[-1][0]%10007)
'PS' 카테고리의 다른 글
| [Python] 백준 29157 - 폭탄 피하기 (0) | 2025.05.09 |
|---|---|
| [Python] 백준 1150 - 백업 (0) | 2025.05.05 |
| [Python] 백준 10220 - Self Representing Seq (0) | 2025.04.22 |
| [Python] 백준 28123 - 삶, 우주, 그리고 모든 것에 관한 궁극적인 질문의 해답 (0) | 2025.04.22 |
| [Python] 백준 3015 - 오아시스 재결합 (0) | 2025.04.21 |