"파이썬으로 구현하는"
시리즈 4
세그먼트 트리
(Segment Tree)
Bottom-Up
오늘은 파이썬으로 Bottom-Up 세그먼트 트리를 어떻게 구현하는지 알아볼 것이다.
지난번에 Top-Down 구현 올리고 계속 올려야지 하다가 1달동안 미뤄졌다;;;;;
다른 블로그들을 보면 Top-Down이 Bottom-Up 보다 이해하기 쉽다고 한다.
개인차일 수도 있는데, 나는 개인적으로 Bottom-Up이 훨씬 이해하기도 쉽고 구현도 간단해서 매우매우 좋아한다!!
Bottom-Up의 구현에서는 Top-Down과 인덱스 저장 방식이 약간 다르다.
오늘은 [3, 1, 4, 1, 5, 9, 2]의 7개의 원소를 다뤄보도록 하자.
Bottom-Up 구현에서는 Top-Down과 달리 7개의 원소가 모두 같은 높이의 리프 노드에 있어야 한다(이게 사실 더 직관적이다). 가령 다음과 같이.
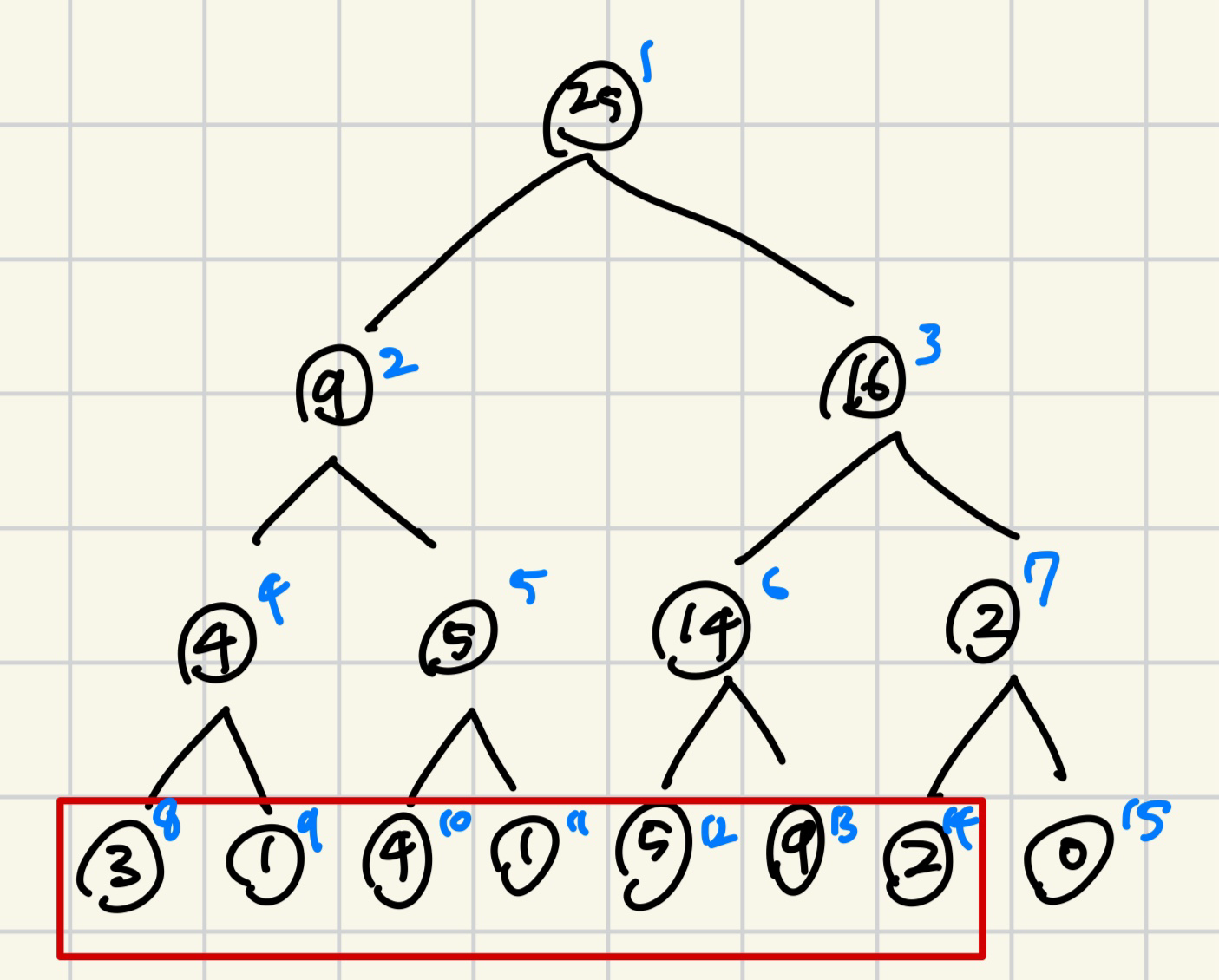
보통 트리를 만들때 리스트를 이용하는데, 인덱스가 1부터 시작하니까 위와 같은 경우에는 길이가 16짜리인 리스트가 필요할 것이다.
필요한 리스트의 길이는 다음과 같이 구할 수 있다.
arr = [3, 1, 4, 1, 5, 9, 2]
N = len(arr)
size = 1
while size < N:
size <<= 1
tree = [0] * (size*2)
size -= 1
개인적으로 math.ceil과 로그를 써서 계산하는 것보다는 이 방법을 추천한다. 절대로 헷갈릴 일이 없다.
마지막에 size에서 1을 빼서 7로 만들었다. 이때 size가 의미하는 바를 잘 이해하고 있으면 좋은데, 리프노드 말고 상위 정보를 저장하고 있는 노드의 개수를 말한다.
size에서 굳이 1을 빼준 이유는 update 함수와 search 함수를 더 쉽게 구현하기 위해서이다.
나중에 보면 알겠지만, 문제에서 리스트의 인덱스가 1부터 시작하면 size에서 1을 빼주고, 0부터 시작하는 문제들의 경우에는 굳이 1을 빼줄 필요가 없다.
그럼 이제 update 함수를 만들어보자. 생각보다 쉽고 간단다.
# 생각보다 간단한 update 구현
def update(idx, diff):
idx += size
while idx:
tree[idx] += diff
idx //= 2
처음에는 idx번째 원소에서 시작한다. 이번 예제에서는 리스트의 인덱스는 1부터 시작한다고 하자. 그러니까 1번째 원소는 3이다.
idx번째 원소의 인덱스를 찾는 방법은, idx에 size를 더해주면 된다!
그리고 이진 포화 트리의 특성을 이용하여 인덱스를 반으로 나눠주면서 위로 올라가주는 것이다.
예를 들어 6번째 원소에 대해서 update를 한다고 하면, 트리상에서의 그 인덱스는 6+7 = 13이 될 것이다.

맨 처음에 트리를 구성할 때는 따로 build 함수를 만든는 것이 아니라, 다음과 같이 update를 N번 해주면 된다. (시간복잡도 ((O(N log N))))
for i in range(1, N + 1):
update(i, nums[i - 1])
print(tree) #[0, 25, 9, 16, 4, 5, 14, 2, 3, 1, 4, 1, 5, 9, 2, 0]
다음으로 만들어볼 것은 search함수이다. 얘는 처음에는 살짝 어려울 수도 있는데 사실 잘 보면 그리 어렵지도 않다.
얘는 약간 이분 탐색틱하게 진행되는 느낌이 없지 않아 있다.
먼저 코드를 보여주겠다.
def search(left, right):
left += size
right += size
ans = 0
while left <= right:
if left % 2 == 1: # 상위 노드에 포함 안되는 경우만 더해준다.
ans += tree[left]
left += 1
left //= 2
if right % 2 == 0:
ans += tree[right]
right -= 1
right //= 2
return ans
원리는 다음과 같다. 예를 들어 2번째 원소(1)부터 6번째 원소(9)까지의 합을 구한다고 쳐보자.
트리상에서의 인덱스는 코드에서도 볼 수 있듯이 처음에 size를 더해서 구해준다. 그 값은 처음에는 9, 13이다.
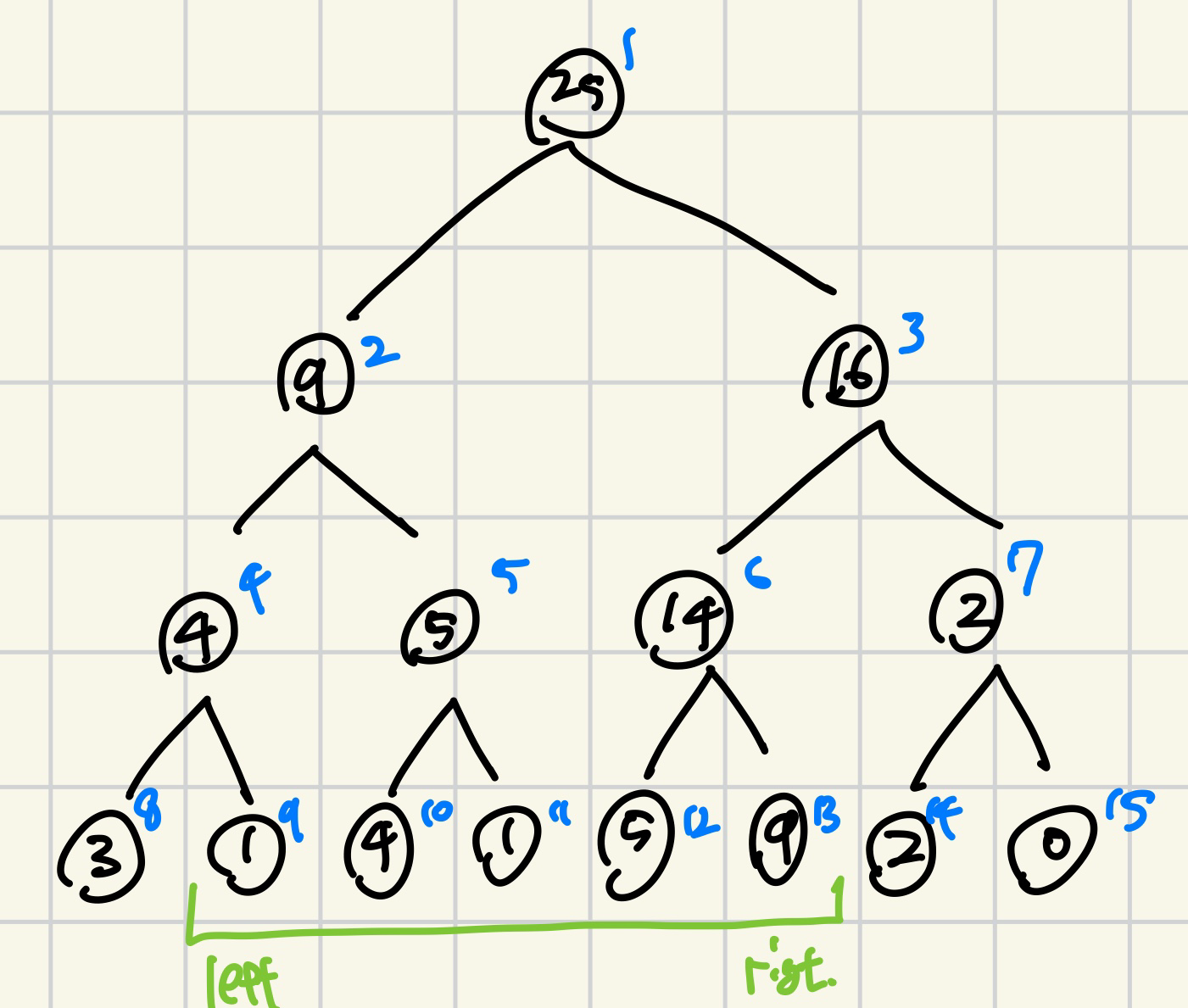
여기서 합을 구하여보자.
10, 11번 노드와 12, 13번 노드는 상위 노드인 5, 6번 노드로 표현할 수 있다.
하지만, 혼자 떨어져있는 9번 노드는 그렇지 않다. 그래서 따로 더해주어야 한다.
따로 떨어져있는지를 어떻게 아는가? 바로 인덱스로 아는 것이다.
left가 가리키고 있는 노드가 포화이진트리 상에서 오른쪽 자식의 노드면 혼자 떨어져있는 노드라고 볼 수 있다.
마찬가지로 right가 가리키고 있는 노드가 포화이진트리 상에서 왼쪽 자식의 노드면 혼자 떨어져있는 노드라고 볼 수 있다.
그런데 포화이진트리의 특성상 오른쪽 자식의 노드는 늘 홀수, 왼쪽 자식의 노드는 짝수이므로 이를 이용해서 혼자 떨어져있는 경우에만 더해주는 것이다.
그리고 다음 탐색 부분으로 넘어가주어야 하는데,
만약 홀로 떨어져있지 않은 노드면 그냥 //=2 를 해주면 되는데, 홀로 떨어져있는 경우 left는 1을 더하고 나누기 2, right는 -1을 빼고 나누기 2를 해야 한다.
이 이유는 아래 그림을 그려보면 알 수 있다.
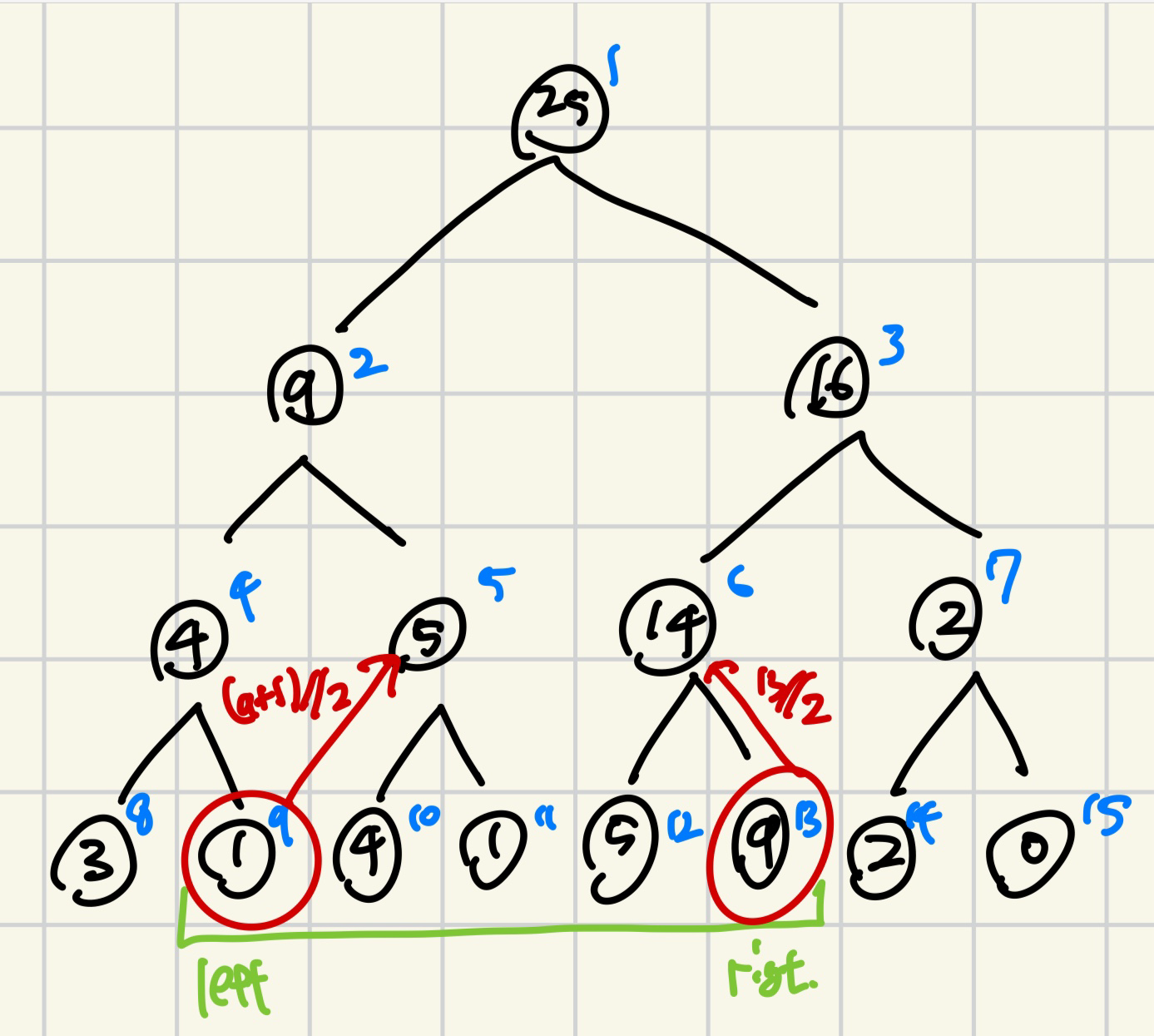
그럼 구현이 다 끝났다!
전체 코드는 다음과 같다.
arr = [3, 1, 4, 1, 5, 9, 2]
N = len(arr)
# 바텀업의 경우에는 인덱스 저장 방식이 살짝 다르다.
# 2**k가 맨 하단이 되는데 이 값이 N보다 커서 맨 아래쪽에 일렬로 nums가 저장되는 방식.
size = 1
while size < N:
size <<= 1
tree = [0] * (2 * size)
size -= 1
# 예를들어, 현재 N = 10이다. 그러면 최소 10개의 저장공간이 필요하다.
# 그러면 size가 16이 될때까지 해주고 저장공간은 두 배인 32을 할당해준다.
# 그리고 size에서 1을 빼는데, 이건 트리 윗부분의 사이즈를 의미한다
# 사이즈에서 1을 빼준 이유는 나중에 업데이트를 쉽게 하기 위해서.
# 생각보다 간단한 update 구현
def update(idx, diff):
idx += size
while idx:
tree[idx] += diff
idx //= 2
for i in range(1, N + 1):
update(i, nums[i - 1])
print(tree)
def search(left, right):
left += size
right += size
ans = 0
while left <= right:
if left % 2 == 1: # 상위 노드에 포함 안되는 경우만 더해준다.
ans += tree[left]
left += 1
left //= 2
if right % 2 == 0:
ans += tree[right]
right -= 1
right //= 2
return ans
코드가 엄청엄청 간단하다. 매개변수도 별로 없어서 내가 개인적으로 애용하는 구현이다.
심지어는 속도도 재귀에 비해 엄청 빠르다.
'파이썬으로 구현하는 시리즈' 카테고리의 다른 글
| [파이썬으로 구현하는] 분할 정복을 이용한 거듭제곱 (0) | 2025.05.17 |
|---|---|
| [파이썬으로 구현하는] 매내처(Manacher) (1) | 2025.04.28 |
| [파이썬으로 구현하는] 세그먼트 트리(Segment Tree) - Top-Down (0) | 2025.04.11 |
| [파이썬으로 구현하는] 분리 집합(Disjoint Set) (0) | 2025.04.05 |